Python is a versatile programming language popular for its readability and ease of use, especially when performing mathematical operations. One powerful arithmetic operator commonly used in Python is the modulo operator, denoted by the percent sign (%).
The Python modulo operator (%) calculates the remainder of a division operation between two numbers. This has several applications in programming, mathematical calculations, and more. Python also allows developers to customize the modulo operator’s behavior by implementing the __mod__() special method in their classes.
In this article, we’ll be looking at the different ways can use the modulo operator when writing Python code.

How to Use the Python Modulo Operator in Python
The modulo operator in Python is a versatile and often overlooked tool that can provide a wealth of functionality to your programs.
At its most basic, it provides a way to determine the remainder of an arithmetic division operation, but its usefulness extends far beyond that. It can also be utilized in various scenarios, such as determining whether a number is even or odd, implementing cyclic or wrap-around logic where values that exceed a certain threshold roll over to start again, or formatting strings to a certain length.
Python offers the modulo operator and several other mathematical methods for performing remainder operations. In this section, we’ll go over some of them.
1. Modulo Operator (%)
The modulo operator, represented by the % symbol, is used in Python to calculate the remainder of a division. It’s considered an arithmetic operation alongside other standard operations like +, –, /, *, and //.
Here’s how it works:
remainder = 7 % 3
print(remainder) # Output: 1In the example above, the modulo operator returns the remainder after dividing 7 by 3.
In most programming languages, the modulo operands must be either negative or positive integers. However, in Python, it can work with floats as well:
remainder_float = 3.14 % 2
print(remainder_float) # Output: 1.14We can see that the modulo operator returns a float value.
2. math.fmod()
The math.fmod() function is an alternative to the Python modulo operator, particularly for floating point numbers.
It’s recommended by the official Python documentation for negative operands due to its consistent behavior when there is a negative number among the operands.
Here’s how it works:
import math
result = math.fmod(-5.5, 3)
print(result) # Output: -2.5In the above example, one of the operands has a single floating point value, so the modulo operator returns a floating point value.
The distinction between % and math.fmod() is more pronounced with negative operands, as the % operator may return different results. We’ll explore this behavior more in a later section.
3. decimal.Decimal()
For even more precision, particularly when working with floating-point numbers, Python provides the Decimal module. The Decimal class allows you to perform exact arithmetic operations, including modulo, with high precision and control over rounding.
Here’s how it works:
from decimal import Decimal
result_decimal = Decimal("3.14") % Decimal("2")
print(result_decimal) # Output: 1.14
Using the Decimal.decimal class can help reduce the accumulation of rounding errors when working extensively with floating-point numbers.
4. divmod()
The divmod() function operates as a sort of extension of the % operator. It takes in two numbers and returns a tuple containing the quotient and the remainder from when the first number is divided by the second.
Let’s look at some examples:
a = divmod(7, 2)
b = divmod(-77, 6)
c = divmod(12.5, 3)
print(a, b, c)
In c, we can see that the divmod() function returns a tuple of floating point numbers if one of the operands is float.
5. __mod__() Method
The mod__() Method is a “magic ” method you can implement in your Python class. It implements the % operator for the objects belonging to that Python class. The remainder returned can be anything from a string to an actual numeric value.
Let’s look at an example:
class fruit:
def __mod__(self, other):
return 'This is the __mod__() function'
a = fruit()
b = fruit()
print(a%b)
print(b%3)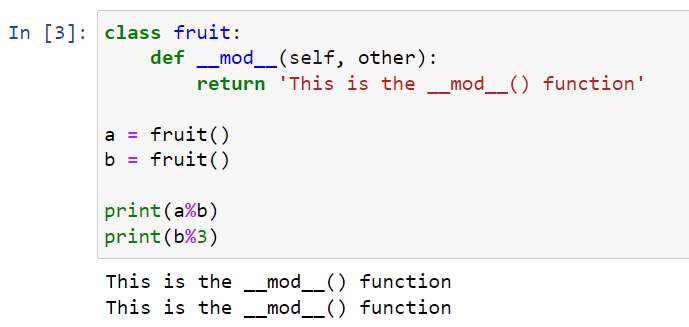
Or let’s look at a more practical example:
class Workers:
def __init__(self, name, age):
self.age = age
self.name = name
def __mod__(self, other):
return self.age%other
a = Workers('john', 34)
print(a%10)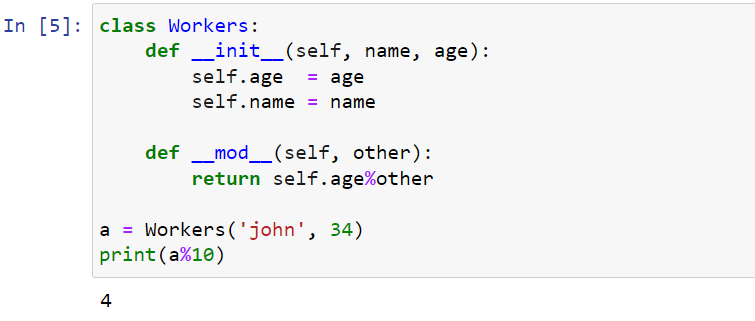
In summary, Python offers various options for calculating the modulo, including the versatile % operator, the math.fmod() function, math.divmod() function and the precise Decimal.decimal class.
You can also implement your own custom modulo behavior using the mod__() method. Depending on the specific needs of your code, each option presents its own benefits and trade-offs.
In the next section, we’ll take a look at some examples of modulo arithmetic in Python.
Examples of Modulo Arithmetic in Python
The modulo operator can be used in arithmetic operations between several types of numeric values. Some of them include:
1. Integer Division
When working with integers, the Python modulo operator functions as expected:
5 % 2 # Returns 1 (5 divided by 2 is 2, remainder 1)
8 % 3 # Returns 2 (8 divided by 3 is 2, remainder 2)
Modulo can also be used to check if a number is even or odd:
number = 7
if number % 2 == 0:
print("Even")
else:
print("Odd")
2. Floating Point Division
The Python modulo operator can also handle floating-point values:
8.0 % 3.0 # Returns 2.0 (8.0 divided by 3.0 is 2, remainder 2.0)
12.3 % 5.0 # Returns 2.3 (12.3 divided by 5.0 is 2, remainder 2.3)
When performing modulo operations with mixed numeric values (integers and floating-point numbers), the result will be a floating-point number:
8 % 3.0 # Returns 2.0 (8 divided by 3.0 is 2, remainder 2.0)
12.3 % 5 # Returns 2.3 (12.3 divided by 5 is 2, remainder 2.3)
3. Negative Numbers
Python modulo operator also behaves differently when dealing with negative numbers compared to some other programming languages. It follows the “floored division” rule, which means the remainder will have the same sign as the divisor:
- When the divisor is positive:
-15 % 4 # Returns 1 (-15 divided by 4 is -4, remainder 1) - When the divisor is negative:
15 % -4 # Returns -3 (15 divided by -4 is -3, remainder -3)
The math.fmod() function behaves quite differently from the % operator in this respect. It always returns a negative number, unless the divisor is negative.
Then, it returns a positive number. Let’s take a look at some examples of this behavior:
a = math.fmod(22, -7)
b = math.fmod(-8, 3)
c = math.fmod(-17, 5)
d = math.fmod(-22, -3)
print(a, b, c, d)
We can see that only a and d are positive because their divisors are negative operands. It’s essential to understand and consider this behavior when using the modulo operation with negative numbers.
To further your understanding of the modulo and other arithmetic operators, we’ll go over operator precedence in Python in the next section!
Operator Precedence in Python
In Python, operator precedence determines the order in which arithmetic operators are executed in an expression. This order of execution is essential, as it can impact the result of the expression.
The modulo operator % shares the same level of precedence as the multiplication *, division /, and floor division // operators. Here is a summary of Python operator precedence, from highest to lowest:
- Parentheses ()
- Exponentiation **
- Bitwise NOT ~
- Multiplication *, Division /, Floor Division //, and Modulo %
- Addition + and Subtraction –
- Bitwise Shift Left << and Shift Right >>
- Bitwise AND &
- Bitwise XOR ^
- Bitwise OR |
- Comparison Operators (<, <=, >, >=, !=, ==)
- Logical NOT not
- Logical AND and
- Logical OR or
When operators share the same precedence, such as %, *, /, and //, Python evaluates them from left to right. However, to ensure a particular order of execution or to make the code more readable, use parentheses.
Expressions enclosed in parentheses will be evaluated first, prior to any other operators of equal or greater precedence. For example, consider the following expression:
result = 100 / 10 * 10 % 7
To clarify the order of execution, use parentheses:
result = ((100 / 10) * 10) % 7
By understanding and using operator precedence in Python, you can write clearer and more accurate expressions when working with the modulo operator and other operators.
Handling Exceptions With the Python Modulo Operator
When working with the Python modulo operator, it’s important to handle any exception that may arise during execution.
In this section, we’ll discuss how to handle ZeroDivisionError and other general exceptions while using the modulo operator in Python.
ZeroDivisionError is a Python exception raised when the right operand of the modulo operation is zero. It’s a subclass of the ArithmeticError exception class.

To handle this exception, you can use the try and except statements. The code that may raise an exception is enclosed within the try block, and the handling code is placed in the except block.
Here’s an example:
try:
result = 10 % 0
except ZeroDivisionError:
print("Cannot perform modulo operation with zero divisor.")
In this example, if the right operand is zero, the ZeroDivisionError exception is caught, and the specified error message is printed.
Apart from ZeroDivisionError, other exceptions may arise during the execution of the modulo operation. To handle any unforeseen exceptions, you can catch the base Exception class.
This ensures that any exception that inherits from Exception will be caught and handled. Here’s an example:
try:
result = 10 % "a"
except ZeroDivisionError:
print("Cannot perform modulo operation with zero divisor.")
except Exception as e:
print(f"An error occurred: {e}")
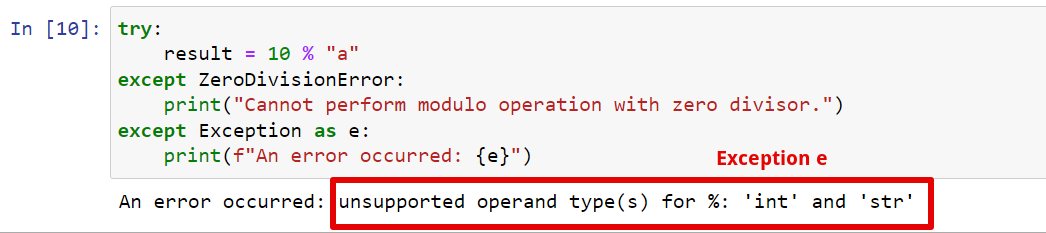
In this case, if an exception is of type ZeroDivisionError, the first error message is printed. However, if another type of exception is raised, the second except block will catch it, and the corresponding error message will be displayed.
Keep in mind that it’s preferable to catch specific exceptions rather than the base Exception class, as doing so allows for better control and handling of errors. By catching specific exceptions, you can provide customized messages and actions for each error case.
You can learn more about Python Exceptions in our Python Try Except article.
In summary, when working with Python modulo operation, always be prepared to handle exceptions such as ZeroDivisionError and other general exceptions.
Utilize try and except statements to provide appropriate error messages and actions for each case, making your code more robust and maintainable.
In the next section, we’ll take a look at how you can use the modulo operator in Python functions.
Using Modulo in Python Functions
The modulo operator % in Python is a versatile tool that can perform several roles in functions. It can be used with various data types such as integers and floats, and applied in a wide range of contexts like condition checking and more.
In this section, we’ll go over some of those contexts.
1. Function With Modulo Arguments
You can create functions that take arguments and use modulo operation within the function. Consider a simple function that checks if a number is even or odd:
def is_even(num):
return num % 2 == 0
In this example, the function is_even takes an integer as the argument, applies the modulo operator % with 2, and checks if the result is equal to 0. If so, it returns True, indicating that the number is even, otherwise False, implying that it’s odd.
2. Modulo in Lambda Functions
Lambdas, or anonymous functions, are another place where modulo can be utilized. These are short, single-line functions that do not require a formal def and return syntax. Here is the same example as before using a lambda:
is_even = lambda num: num % 2 == 0
This code creates the same is_even functionality but with a more concise syntax thanks to lambda expressions.
3. Incorporating Modulo Into Custom Functions
You can also create custom functions that involve modulo operations in various ways, such as applying modulo to a list of numbers.
As an example, let’s make a function that takes a list of numbers and a divisor and returns a filtered list containing only numbers divisible by the divisor:
def filter_divisible(numbers, divisor):
return [num for num in numbers if num % divisor == 0]
numbers_list = [1, 2, 3, 4, 5, 6, 7, 8, 9]
result = filter_divisible(numbers_list, 3)
print(result) # Output: [3, 6, 9]
In this code, the filter_divisible function makes use of list comprehension and the modulo operator % to filter out numbers that are not divisible by the provided divisor.
By incorporating the modulo operator in Python functions and lambda expressions, you can efficiently solve various problems and create versatile functionality in your code.
Next, we’ll discuss how you can use the modulo operator with loops and range in Python.
How to Use the Modulo Operator With Loops and Range
In Python, loops are useful in executing a block of code for a specific number of iterations. The two most common types of loops are for and while, and they can easily be utilized with the modulo operation.
range() is a built-in function in Python that produces a sequence of numbers. By default, this sequence starts from 0, increments by 1, and ends at a specified number.
It can be particularly handy when combined with for loops as it allows us to control the number of iterations.
Here’s an example of using loops and range with the Python modulo operation:
for i in range(0, 10):
if i % 2 == 0:
print(f"{i} is an even number")
else:
print(f"{i} is an odd number")
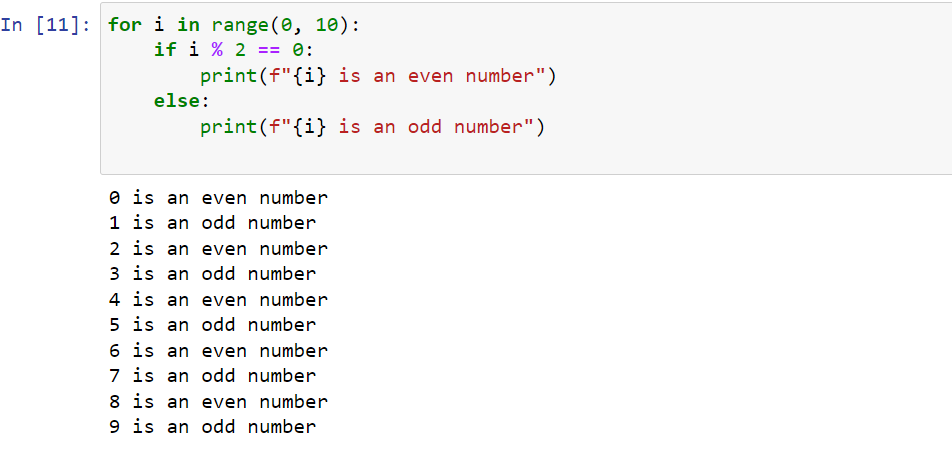
In this example, we use a for loop and range() to iterate over numbers from 0 to 9. The modulo operation (i % 2) helps us determine if the number is even or odd.
You can check out a real-life application of the range() function in our video on finding similar matches with Euclidean distance using Python in Power BI:
We can also use a while loop in combination with the modulo operation, as shown in the example below:
i = 0
while i < 10:
if i % 2 == 0:
print(f"{i} is an even number")
else:
print(f"{i} is an odd number")
i += 1
Here, the while loop iterates and performs the modulo operation as long as the condition i < 10 holds true.
You can also create custom range functions with a specified step, like so:
def custom_range(start, end, step):
i = start
while i < end:
yield i
i += step
for i in custom_range(0, 10, 2):
print(f"{i} is an even number")
This custom custom_range function generates a range of numbers from a given start to an end with a defined step. In this example, it outputs even numbers between 0 and 10.
Alright, we’ve covered a lot of ground so far. For our final section, we’ll go over some performance considerations when working with Python’s modulo operator.
Performance Considerations With Python’s Modulo Operator
When working with Python’s modulo operator in your code, it’s important to consider the performance implications. The performance of the modulo operation can depend on various factors, such as the size of the numbers being used and the specific use case.
One aspect to consider is the choice between using the modulus operator (%) or the divmod() function. Although both methods can be used to achieve the same result, their performance will differ depending on the situation.
In some tests, the modulus operator has been reported to outperform the divmod() function due to the latter requiring a global lookup each time it is used.
However, binding divmod() to a local variable can improve its performance to some extent. On the other hand, the modulus operator doesn’t have this bottleneck as it does not need to preserve intermediate results.
Another factor to keep in mind is the cost of system calls. Although Python itself doesn’t involve system calls when calculating the modulus, excessive or inefficient use of the modulo operation may result in slow performance, indirectly affecting the overall efficiency of your code.
To avoid this, try optimizing your code by refactoring, using built-in functions or libraries, and remembering to use multiple assignments when possible.
Final Thoughts
In summary, the Python modulo operator (%) is a versatile and essential arithmetic operator that returns the remainder of a division between two numbers. It is widely used in various programming scenarios and has numerous applications.
Here are some key takeaways:
- The modulo operator % is used in Python to obtain the remainder of a division.
- When working with float values and negative operands, the math.fmod() function is a more reliable option.
Remember to apply the modulo operator thoughtfully and consider its caveats when working with specific scenarios or data types. By doing so, you can harness the full potential of this mathematical operation in your Python programming. Happy coding!