Mapping functions over NumPy arrays is a popular technique in data processing and manipulation. It involves the application of a specific function to each element in the array, making it an efficient way to perform element-wise operations.
You can map a function over a NumPy array by passing the array into the function using NumPy’s vectorize function, or by using the map function. You can also do this by iterating over the NumPy array with a for loop or using list comprehension.
Utilizing these methods not only simplifies the code but also optimizes the performance of data manipulation tasks. As a result, it’s crucial for programmers and data scientists to master these techniques to make the most of the NumPy library’s capabilities.
This article will discuss the different methods to map a function over a NumPy array. We’ll also provide insights into their advantages and recommended use cases.
Let’s dive in!
Understanding NumPy Arrays
NumPy arrays are fundamental data structures in scientific computing with Python. These multidimensional arrays provide a powerful, efficient way to store, manipulate, and perform operations on large datasets.
You can see how powerful they are in this video on how to resample time series data using Pandas to enhance analysis:
Compared to native Python lists and arrays, NumPy arrays come with various built-in functions, significantly improving their performance. In fact, the data structures in the other libraries like Pandas are all built on the NumPy library.
How to Import NumPy
To get started with NumPy, you need to install it using pip:
pip install numpyOnce installed, you can import the library into your Python script as follows:
import numpy as npBy convention, the np alias is used as a shorthand when working with NumPy arrays and functions.
How to Map a Function Over a NumPy Array
Mapping a Python function over a NumPy array allows you to apply a specific operation to each element in the array. Let’s look at some ways you can achieve this:
1. Passing the Array to the Function
The simplest way to map a function over a NumPy array is to pass the array straight into the function. However, this comes with a caveat.
Let’s look at an example with a one-dimensional array:
import numpy as np
# Create a NumPy array
arr = np.array([1, 2, 3, 4, 5])
# Define a function to square elements
def square(x):
return x**2
# Pass the NumPy array into the function
squared_arr = square(arr)
print(squared_arr)Output:
[ 1 4 9 16 25]This code will output [ 1 4 9 16 25], the squared elements of the original array arr. Next, let’s look at how this will work in a multi-dimensional array.
data = np.array([[1, 2, 3, 4], [5, 6, 7, 8]])
#define an anonymous function
a = lambda t: t +10
b = a(data)
print(b)Output:
[[11 12 13 14]
[15 16 17 18]]Let’s look at another example where the function doesn’t involve mathematical operators or a return statement. Let’s map a function that prints out the NumPy array data and their data types.
arr = np.array([1, True, 'ball'])
def type_arr(x):
print(x, type(x))
type_arr(arr)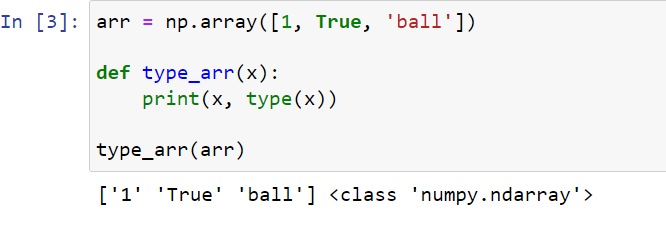
We can see that the result isn’t what we were expecting. In this case, simply passing the array into the function isn’t enough to map the function over each item of the entire array.
Passing the array into the function only works for mathematical calculations because mathematical operators are NumPy ufuncs. So, the functions are automatically vectorized. You can read more about these functions here.
In the next sections, we’ll take a look at ways we can pass both arithmetic and non-arithmetic functions over NumPy arrays.
2. Using the Vectorize Function
To map a function over a NumPy array, the vectorize function can be utilized. This function is available within the NumPy library and can be used to create a vectorized version of a specified function.
The vectorized version of the function takes in a sequence and applies the function’s logic over each item of the sequence. Here’s an example of defining your own function and then converting it to a vectorized function:
import numpy as np
# Define a simple lambda function
my_lambda = lambda x: np.sin(x)
# Create a vectorized version of the lambda function using np.vectorize()
my_func = np.vectorize(my_lambda)In this example, my_lambda is a simple lambda function that computes the sin of each element in the NumPy array. my_func is the vectorized version of it, which has been created using np.vectorize().
Once you’ve created the vectorized function, you can use it to easily map the function over a NumPy array. The following example demonstrates this:
# Create a sample NumPy array
array = np.array([0, np.pi / 4, np.pi / 2, 3 * np.pi / 4])
# Apply the vectorized function to the NumPy array
result = my_func(array)
print(result)The output of this code snippet would be:
[0.00000000e+00 7.07106781e-01 1.00000000e+00 7.07106781e-01]
As expected, the sin function has been mapped over each element of the NumPy array, and the result has the same shape as the input array.
We can also use the np.vectorize() function for mapping over multi-dimensional arrays:
def myfunc(a, b):
if a > b:
return a - b
else:
return a + b
vfunc = np.vectorize(myfunc)
result = vfunc(np.array([[1, 2, 3], [1, 2, 3]]), 2)In this example, myfunc is a user-defined function that takes two arguments, a and b, and returns a result based on their values.
3. Expanding the Input Function
In some cases, you might need to expand the input function to accommodate additional arguments or keyword arguments (kwargs) that are not directly related to the input data.
To facilitate this functionality, numpy.vectorize() can be utilized with additional args and *kwargs parameters:
import numpy as np
def power(x, n):
return x ** n
# Declare the function with additional arguments as `pyfunc`
vfunc = np.vectorize(power, excluded=['n'])
# Applying the function to NumPy array with keyword arguments
array = np.array([1, 2, 3, 4, 5])
result = vfunc(array, n=3)
print(result) Output:
[ 1 8 27 64 125]Specifying Arguments and Keyword Arguments
When working with the numpy.vectorize() function, you can specify the needed arguments during initialization. You can use these parameters to control the function behavior and improve the performance in certain cases.
For example, cache results using the cache parameter to improve performance for expensive computations:
import numpy as np
def expensive_function(x):
# Some expensive computation
return x ** 2
# Specify caching during vectorization
vfunc = np.vectorize(expensive_function, cache=True)
# Apply the vectorized function to a NumPy array
array = np.array([1, 2, 3, 4, 5])
result = vfunc(array)
print(result)Output:
[ 1 4 9 16 25]Performance Considerations
While using vectorize() can simplify your code when applying a function to a NumPy array, it’s essential to consider the performance implications. The vectorize function is not always the most efficient way to map a function over a NumPy array since it operates on Python scalars, which may have added overhead.
It’s always a good idea to compare the performance of using vectorize() with alternative methods. You can leverage NumPy’s built-in functions or implement a loop with NumPy operations to see if the performance can be improved.
4. Using the Map Function
The map function returns an iterable after applying a function to every item of a Python sequence. To use it place a NumPy array and the function as arguments in the map function and get a map object as a result.
Let’s look at its Python syntax:
result = map(<function>, <numpyarray>)Note: The map function returns a map object. So, you’re going to have to transform that function back into a Python iterable like a list, then back into a NumPy array.
Let’s illustrate this with an example. Let’s write a function to multiply all the numbers by 3.
def x(a):
return 3*a
arr = np.array([7, 5, 23, 16])
result = np.array(list(map(x, arr)))Output:
[21 15 69 48]As you can see, we had to wrap the map function in both a list() and np.array() function to get a NumPy array as a result.
5. Using a For Loop
We can also use the for loop to map a function all over a NumPy array. Let’s look at an example:
def funcx(a):
return a+ 5
a = np.array([9,5,3,1])
#Create a Numpy array similar to arr to store the results
result = np.arr_like(arr)
for i in range(len(arr)):
result[i] = funcx(arr[i])
#display numpy array
print(result)Output:
[14 10 8 6]We use the for loop to apply the function to each element of the Numpy array, then we add the result to a new array.
6. Using List Comprehension
List comprehension is a quick and easy way for mapping a function over a Numpy array. Let’s take a look:
add = lambda x: x+10
a = np.array([9,5,3,1])
result = np.array([add(x) for x in a])
print(result)Output:
[19 15 13 11]As we can see, we have shortened our previous example to just a few lines by using the list comprehension method.
We can also use nested list comprehension to map over a multi-dimensional array. Here’s an example:
data = np.array([[1, 2, 3, 4], [5, 6, 7, 8]])
squared_data = np.array([[xi ** 2 for xi in row] for row in data])
print(squared_data) Output:
[[ 1 4 9 16]
[25 36 49 64]]Final Thoughts
To summarize, mapping a function over a NumPy array opens up a world of possibilities for data manipulation and analysis. By harnessing the power of the functions above you can efficiently apply functions to NumPy arrays and process data in a concise and elegant manner.
So go ahead, explore the possibilities, and unlock the full potential of your NumPy arrays! For more fun NumPy features, you can check out our NumPy Cheat Sheet.
You can also check out this fun article on How to Normalize NumPy Arrays.
Frequently Asked Questions
What is the Most Efficient Way to Map a Function Over a Numpy Array?
There is no clear answer to this question. It all depends on the code in the Python function and the Python and NumPy versions.
For some versions, the vectorize() function might be the fastest, while for some using the direct approach might be optimal.
What Does a Vectorized Function Return?
A vectorized function takes in a NumPy array and returns a NumPy array. The map function returns a mapobject that you will have to transform into a list, then a NumPy array.