If you’ve been working with Python for data analysis or machine learning, you’ve likely come across NumPy arrays. They’re a powerful tool for handling numerical data, but sometimes, the data within these arrays needs to be adjusted or ‘normalized’ to be effectively used in your algorithms. But what does it mean to normalize an array?
To normalize a NumPy array, you have to adjust the values in the array so that they fall within a certain range, typically between 0 and 1, or so that they have a standard normal distribution with a mean of 0 and a standard deviation of 1. This is often done in the field of machine learning and data analysis to ensure that all input features have the same scale.

In this article, we’ll explore how you can normalize a NumPy array in Python. We’ll look at the different methods you can use to normalize a NumPy array and also look at examples to help you better understand the concept.
Let’s get into it!
What Are the Basics of Normalization in Python?
Before we implement normalization in Python, you must understand what normalization means.

Therefore, in this section, we’ll go over what is normalization and its core concepts.
What is Normalization?
Normalization is a process that scales and transforms data into a standardized range. This is done by dividing each element of the data by a parameter. The parameter can be the maximum value, range, or some other norm.
You can normalize NumPy array using the Euclidean norm (also known as the L2 norm). Furthermore, you can also normalize NumPy arrays by rescaling the values between a certain range, usually 0 to 1.
In Python, the NumPy library provides an efficient way to normalize arrays. This includes multi-dimensional arrays and matrices as well.
Why is Normalization Important?
Normalization is important as it ensures that different features are treated equally when comparing and analyzing data. You can use it to eliminate potential biases or discrepancies that might arise due to varying scales.
What Are Norms?
The parameter that you use for normalization can be different norms, such as the Euclidean norm (L2), the Manhattan norm (L1), or the max norm (L_inf). You use norms to calculate the magnitude of a vector or matrix. These are then used as a scaling factor to normalize the data.
When working with matrices, we often use the Frobenius norm, which is a generalization of the Euclidean norm for multi-dimensional arrays.
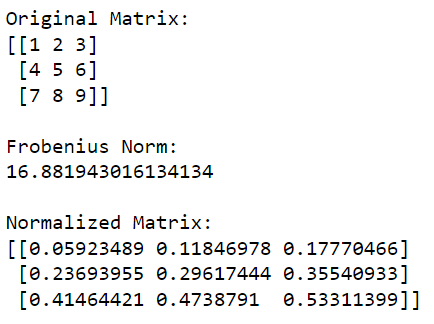
The following example shows the normalization of a matrix using the Frobenius norm:
import numpy as np
# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
# Calculate the Frobenius norm
frobenius_norm = np.linalg.norm(matrix, 'fro')
# Normalize the matrix
normalized_matrix = matrix / frobenius_norm
print('Original Matrix:')
print(matrix)
print('nFrobenius Norm:')
print(frobenius_norm)
print('nNormalized Matrix:')
print(normalized_matrix)This Python code will first import NumPy library and use it to create a matrix. It then calculates the Frobenius norm of the matrix and then divides each element in the matrix by this value to normalize it.
The output of this code is given below:
What is Normalization in Machine Learning?
In machine learning, normalization is an important preprocessing step as it improves the performance of algorithms.
When performing gradient-based optimization techniques, you’ll find that optimized features tend to converge more quickly and efficiently. This is because it reduces the risk of poor scaling or vanishing gradients.
What are the Techniques of Normalization in Python?
You can perform normalization of NumPy arrays in a number of ways. However, some methods are more popular than others due to their high efficiency.

For this section, we’ll look at the three widely used normalization techniques:
Min-Max Scaling
L1 Normalization
L2 Normalization
1. How to Perform Min-Max Scaling
Min-max scaling is also known as linear normalization or feature scaling. In min-max scaling, we scale the values of a NumPy array so that they fall within a specified range, typically between 0 and 1.
To do this, you subtract the minimum value from each element and divide the result by the difference between the maximum and minimum values.
You can represent the min-max scaling mathematically as:
x' = (x - min(x)) / (max(x) - min(x))The following example demonstrates how you can perform min-max scaling using the NumPy library:
import numpy as np
# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
# Perform min-max scaling
min_val = np.min(matrix)
max_val = np.max(matrix)
scaled_matrix = (matrix - min_val) / (max_val - min_val)
print('Original Matrix:')
print(matrix)
print('nMin-Max Scaled Matrix:')
print(scaled_matrix)This code will first import NumPy and then compute the minimum and maximum values in the matrix, which it then scales such that all values are between 0 (corresponding to the original minimum value) and 1 (corresponding to the original maximum value).
The output of this code is given below:

Min-max scaling is a very common form of scaling in machine learning and data preprocessing.
2. How to Perform L1 Normalization
L1 normalization employs the L1-norm, which is the sum of the absolute values of the array elements. This is particularly useful for sparse matrices. It ensures that the sum of the absolute values of the normalized array elements equals 1.
The formula for L1 normalization is:
x' = x / sum(|x|)The following example shows how you can perform L1 normalization using NumPy:
import numpy as np
# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
# Perform L1 normalization
l1_norm = np.linalg.norm(matrix, 1, axis=1, keepdims=True)
l1_normalized_matrix = matrix / l1_norm
print('Original Matrix:')
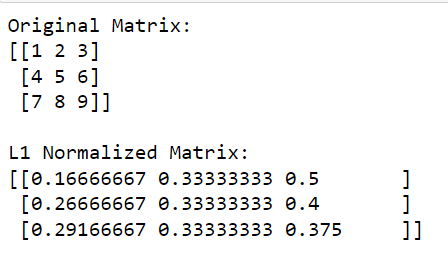
print(matrix)
print('nL1 Normalized Matrix:')
print(l1_normalized_matrix)In this code, np.linalg.norm(matrix, 1, axis=1, keepdims=True) calculates the L1 norm for each row (this is done by specifying axis=1).
This operation will return a column vector where each element is the L1 norm of the corresponding row. By dividing the original matrix by these norms (performing the division element-wise), we obtain the L1 normalized version of the matrix.
The output is given below:
3. How to Perform L2 Normalization
L2 normalization uses the L2-norm, which is the square root of the sum of the squared array elements.
This method converts the normalized array into a unit vector with a 2-norm of 1. L2 normalization is useful for dimensional reduction and ensures equal importance for all features.
The formula for L2 normalization is:
x' = x / sqrt(sum(x^2))This is how you can perform L2 normalization using NumPy:
import numpy as np
# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
# Perform L2 normalization
l2_norm = np.linalg.norm(matrix, 2, axis=1, keepdims=True)
l2_normalized_matrix = matrix / l2_norm
print('Original Matrix:')
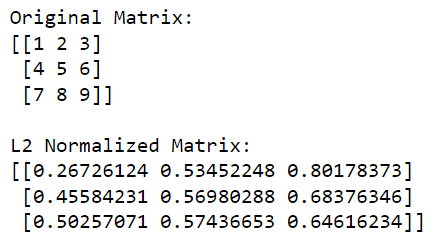
print(matrix)
print('nL2 Normalized Matrix:')
print(l2_normalized_matrix)In this code, np.linalg.norm(matrix, 2, axis=1, keepdims=True) calculates the L2 norm (Euclidean norm) for each row (this is done by specifying axis=1). This operation will return a column vector where each element is the L2 norm of the corresponding row.
By dividing the original matrix by these norms (performing the division element-wise), we obtain the L2 normalized version of the matrix.
The output is given below:
Alright, now that we’ve gone over the popular ways to create a normalized array using NumPy, let’s take a look at how you can do the same using other Python libraries in the next section.
How to Use Scikit-Learn for Normalization in Python
Scikit-learn is a powerful Python library for machine learning. It provides several tools for data preprocessing.

One tool you can use is the sklearn.preprocessing module, which offers various techniques to perform normalization. There are many different scaler functions, transformers, and normalizers available. However, we’ll focus on MinMaxScaler and the normalize function.
To preprocess data with scikit-learn, you mainly use the transformer API. This includes the fit, transform, and fit_transform methods.
1. How to Normalize Array Using MinMaxScaler
The MinMaxScaler is a scaler that normalizes data to a specified range, usually [0, 1].
The formula for MinMaxScalar is given below:
scaled_value = (value - min_value) / (max_value - min_value)To implement the MinMaxScaler, you can follow these steps:
Import the required libraries:
import numpy as np from sklearn.preprocessing import MinMaxScalerdata = np.array([[1., 2., 5.], [3., 6., 8.], [5., 10., 12.]])Instantiate the MinMaxScaler and fit it to the data:
scaler = MinMaxScaler() scaler.fit(data)Transform the data using the transform or fit_transform method:
normalized_data = scaler.transform(data)
The output of this code is given below:

As you can see in the output that the MinMaxScalarMatrix only has values ranging from 0 to 1.
2. How to Perform In-Place Row Normalization
You can also use the in-place row normalization as an alternative, using the normalize function.
This method normalizes each input array or feature independently by scaling the vector to a unit norm. By default, the normalize function uses the L2 norm to perform simple normalization, but you can choose other norm options.
The following example demonstrates in-place row normalization:
from sklearn.preprocessing import normalize
import numpy as np
# Initialize your matrix
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]], dtype=float)
# Apply in-place row normalization
normalize(matrix, norm='l2', copy=False)
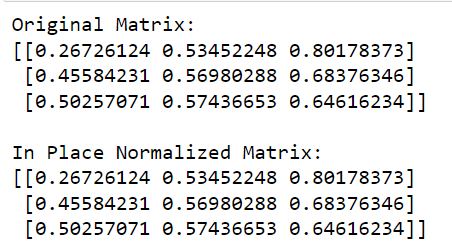
print('L2 Normalized Matrix:')
print(matrix)In this code, we call the normalize function from sklearn, define the norm to use (‘l2’ in this case), and set copy=False to perform in-place normalization.
The output of this code is given below:
To learn more about machine learning in Python, check the following video out:
Final Thoughts
As you further explore data science and machine learning, you’ll find that the normalization process is an essential step in your data preprocessing pipeline.
Firstly, it places different features on a common scale. This makes your models less sensitive to the scale of inputs. It can greatly improve the performance of many machine-learning algorithms.
Secondly, it assists you in speeding up the training process. Some algorithms, especially those based on calculated distance computations, converge faster when data is normalized.
By learning how to normalize data, you equip yourself with a crucial skill. Normalization is a practical tool used routinely in real-world applications. It’ll help you in reducing the likelihood of unexpected results due to outliers or differences in units.
Like any tool, the key to mastering normalization lies in practice. So, don’t hesitate to get your hands dirty and experiment with different datasets and random values. The world of data science is your oyster. Happy coding!