Pi is a fundamental mathematical constant that represents the ratio of a circle’s circumference to its diameter. Leveraging Pi in Python is essential when dealing with geometrical calculations, trigonometry, and various other mathematical operations.
Python offers multiple ways to access and use Pi in calculations. The Math and NumPy libraries are two commonly-used modules that provide Pi as a constant.
There are several other modules that provide the constant. Your choice depends on how much mathematical precision you need and what other calculations your application requires.
This article shows you how to access Pi with four methods, and explains which will best suit your requirements.
Let’s dive into it.
Understanding Pi in Python

Pi (?) represents the ratio of a circle’s circumference (c) to its diameter (d). In simpler terms, ? = c/d.
The value of pi is approximately 3.14159.
Pi is an irrational number, which means that it goes on infinitely without repeating itself. It cannot be expressed as a simple fraction and it does not have an exact decimal representation.
Here are the first few digits of pi to give you an idea of its nature:
3.14159265358979323846...The value of pi is often shortened to just a few decimal places in calculations for practical purposes, such as 3.14 or 22/7.
However, this truncated representation might not be accurate enough for some applications, such as high-precision numeric simulations or specific mathematical proofs.
4 Common Ways to Access Pi in Python

The four most common ways to access a pi in Python are using the:
Math module
NumPy module
SciPy module
cmath module
Keep in mind that while Python’s math.pi constant is accurate enough for most purposes, there are even more accurate approximations available through other libraries. For example, NumPy provides a higher degree of precision.
The choice of which library to use depends on your specific needs and other functionalities you may require from the library. If you are already using NumPy or SciPy in your project, it would be appropriate to use their respective pi constants.
If you need to work with complex numbers, then the cmath module is the best choice.
If you don’t need any additional functionality from these libraries and only require an approximate value of pi, using Python’s built-in math library is probably your best option.
How to Access Pi With the Math Library
The math module in Python allows you to work with the number pi and provides an accurate approximation of up to 15 decimal places.
This is one of Python’s inbuilt modules, which means you don’t have to download and install it separately.
You have two options for importing pi for use in your code:
import math library
import only the pi constant
This code imports the full library:
import math
pi_value = math.piThis code only imports the pi constant:
from math import pi
pi_value = pi3 Ways to Use the Pi Constant With Other Math Functions
Apart from the pi constant, the math module offers many other mathematical functions. These functions can be combined with math.pi to:
calculate the circumference of a circle
calculate the area of a circle
calculate radians and degrees
Let’s look at each in turn.
1. Circumference of a Circle

The circumference of a circle can be calculated using the following formula:
C = 2 ? r
C is the circumference
? is the constant Pi
r is the radius of the circle.
In Python, you can calculate the circumference of a circle by importing the math module and using the pi math constant like this:
import math
radius = 5
circumference = 2 * math.pi * radius
print(circumference)You may also want the Euclidean distance for two points on the circumference. This video shows the calculations:
2. Area of a Circle
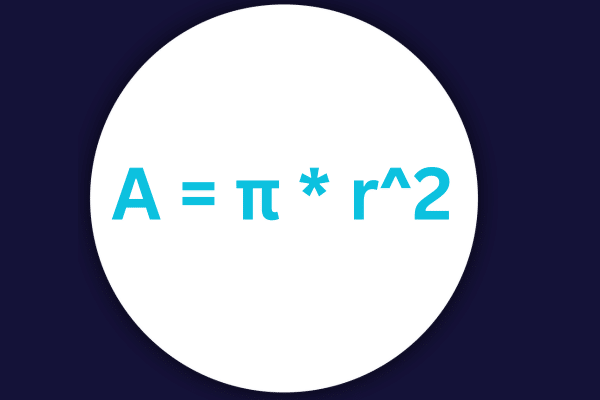
The area of a circle can be calculated using the following formula:
A = ? * r^2
A is the area
? is the constant Pi
r is the radius of the circle.
In Python, you can calculate the area of a circle like this:
import math
radius = 5
area = math.pi * (radius ** 2)
print(area)3. Radians and Degrees

Angles can be measured in two common units: degrees and radians. A full circle comprises 360 degrees or 2? radians. To convert degrees to radians, you can use pi in a simple formula:
Radians = Degrees * (? / 180)
However, the math module also offers a convenient function to convert degrees to radians: the math.radians(). This simplifies your calculations.
Here’s a basic example of how to use the function radians():
import math
angle_degrees = 45
angle_radians = math.radians(angle_degrees)
print(angle_radians)The function returns the calculation based on the inbuilt math Pi constant.
How to Use Pi With the NumPy Module
NumPy is a popular Python library for working with numerical data. It provides a constant for the mathematical constant pi (approximately 3.14159).
Unlike the math library, NumPy is not a built-in Python module. You can install it using pip, Python’s package manager. The command to install Python NumPy would typically be:
pip install numpyHere is an example of importing the module and accessing the pi NumPy constant:
import numpy as np
pi_value = np.pi
print(pi_value)This code will output the value of the pi variable (3.141592653589793) from the NumPy library.
How to Use Pi With the SciPy Module
SciPy is another widely used Python library for scientific and technical computing. It builds on top of the NumPy library and includes several additional functionalities.
You can install it using pip, Python’s package manager. The command to install SciPy would typically be:
pip install scipyHere is an example of importing SciPy and accessing the pi constant:
import scipy
pi_value = scipy.pi
print(pi_value)This code will return the value of pi (3.141592653589793) provided by the SciPy library.
How to Use Complex Numbers With the cmath Module
Python provides support for complex numbers through the built-in cmath module.
Here is an example of using the pi constant in the cmath module for calculations with complex numbers:
import cmath
# Define a complex number
z = 1 + 1j
# Compute the power of pi using the complex number
result = cmath.exp(z * cmath.pi)
print(result) # Output: (-1-2.8421709430404007e-14j)
Errors and Exception Handling With Pi in Python

When performing calculations with pi in Python, it is always good practice to use proper exception-handling techniques. You may encounter some of the more common calculation errors:
ZeroDivisionError
OverflowError
ArithmeticError
To handle multiple exceptions, you can use the try, except, and finally statements in Python:
try:
# Perform calculation here
except (ZeroDivisionError, OverflowError, ArithmeticError):
# Handle specific errors here
finally:
# Code to be executed regardless of any exceptions
Here is an example of handling errors when calculating the area of a circle:
import math
def calculate_area(r):
pi = math.pi
try:
area = pi * r**2
except (TypeError, OverflowError, ValueError):
area = None
print("Error: Invalid input or calculation failure")
finally:
return area
radius = 5
circle_area = calculate_area(radius)
print(circle_area)
Final Thoughts
You have learned how to access pi using four different Python modules. Depending on your requirements, be sure to pick the one that provides the accuracy that you need.
The many examples in this article cover most of the scenarios you’ll meet in your mathematics calculations. If you need more help, our Python cheat sheet and ChatGPT are great resources.
Happy coding!