Evaluating machine learning models is like testing a student’s knowledge. It helps you measure their accuracy, understand how well they’re learning, and decide if they need to improve.
Model evaluation is a critical process in machine learning, as it allows you to assess the performance and generalization of a trained model. It involves comparing the model’s predictions to actual data to determine its accuracy, precision, recall, and other metrics.
Understanding model evaluation is essential to ensure that the machine learning system you develop will be effective in solving real-world problems.
This article will give you an in-depth understanding of how to evaluate machine learning models and will guide you on best practices for model evaluation.
Let’s dive in!
What is Model Evaluation in Machine Learning?

The model evaluation is the process of quantifying how well a machine learning model performs on a given dataset. It is essential to evaluate the model’s performance to assess its ability to make predictions or decisions on new, unseen data.
Model evaluation involves several important concepts, such as accuracy, precision, recall, F1 score, and area under the curve (AUC). These metrics are used to compare the model’s predictions to the actual outcomes and determine its effectiveness.
How to Evaluate Machine Learning Models

In this section, we’ll go over the following evaluation metrics:
- Accuracy
- Precision
- Recall
- F1 Score
- Confusion Matrix
- Receiver Operating Characteristic (ROC) Curve and Area Under the Curve (AUC)
- Logarithmic Loss
- Mean Squared Error
- Mean Absolute Error
- R-squared
1. Accuracy
Accuracy is one of the most common metrics used to evaluate a model. It represents the proportion of correct predictions made by the model over the total number of predictions. Accuracy is calculated using the following formula:
Accuracy = (True Positives + True Negatives) / (True Positives + False Positives + True Negatives + False Negatives)
Where:
- True Positives (TP) are the number of correct positive predictions (e.g., the model predicted a person has a disease, and they actually do).
- True Negatives (TN) are the number of correct negative predictions (e.g., the model predicted a person does not have a disease, and they actually don’t).
- False Positives (FP), also known as Type I errors, are incorrect positive predictions (e.g., the model predicted a person has a disease, but they don’t).
- False Negatives (FN), also known as Type II errors, are incorrect negative predictions (e.g., the model predicted a person does not have a disease, but they do).
The accuracy metric is easy to understand and can provide a quick overview of a model’s performance. However, it may not be the best metric to use when the dataset is imbalanced. We’ll explore this in the next section.
2. Precision
Precision measures the proportion of true positive predictions among all positive predictions made by the model. It is calculated using the following formula:
Precision = True Positives / (True Positives + False Positives)
Precision is a valuable metric when the cost of false positives is high. For example, in a medical diagnosis system, precision is essential because it tells us how often the model correctly identifies a positive case (e.g., a patient has a disease) and not falsely labeling a negative case as positive.
3. Recall
Recall, also known as sensitivity, measures the proportion of true positive predictions among all actual positive instances in the dataset. It is calculated using the following formula:
Recall = True Positives / (True Positives + False Negatives)
Recall is crucial when the cost of false negatives is high. For example, in a medical diagnosis system, recall is important because it tells us how often the model can correctly identify a positive case out of all the positive cases (e.g., how many patients with the disease are correctly identified).
4. F1 Score
The F1 score is a metric that combines precision and recall into a single value. It is particularly useful when the dataset is imbalanced.
The F1 score is calculated as follows:
F1 Score = 2 * (Precision * Recall) / (Precision + Recall)
The F1 score gives equal weight to both precision and recall and provides a balance between the two metrics.
5. Confusion Matrix
A confusion matrix is a table that is often used to describe the performance of a classification model on a set of test data for which the true values are known.
It allows the visualization of the performance of an algorithm.
The confusion matrix has 4 important components:
- True Positives (TP)
- False Positives (FP)
- True Negatives (TN)
- False Negatives (FN)
The following is an example of a confusion matrix for a binary classification problem:
6. Receiver Operating Characteristic (ROC) Curve and Area Under the Curve (AUC)
The Receiver Operating Characteristic (ROC) curve is a graphical representation of a binary classifier’s performance at various threshold settings. It is created by plotting the true positive rate (TPR) against the false positive rate (FPR) as the threshold changes.
The ROC curve shows the trade-offs between sensitivity and specificity for a given classifier. An ROC curve that lies closer to the top-left corner indicates better performance.
The Area Under the Curve (AUC) is a single scalar value that quantifies the overall performance of the classifier. A perfect classifier will have an AUC of 1, while a random classifier will have an AUC of 0.5.
7. Logarithmic Loss
Logarithmic Loss, also known as cross-entropy loss, is a measure of uncertainty. It measures the performance of a classification model where the predicted output is a probability value between 0 and 1.
The goal is to minimize this value.
The formula for Logarithmic Loss is as follows:
$$ Log Loss = -\frac{1}{N} \sum_{i=1}^{N} \sum_{j=1}^{M} y_{ij} \log(p_{ij}) $$- N: Number of samples in the dataset
- M: Number of classes
- $y_{ij}$: Actual binary indicator if class label j is the correct classification for sample i
- $p_{ij}$: Predicted probability that sample i belongs to class j (output of the classifier)
8. Mean Squared Error
Mean Squared Error (MSE) is a measure of the average of the squares of the errors or deviations. It is a common way to measure the quality of an estimator and is always non-negative.
The formula for Mean Squared Error is:
MSE = 1/n * ?(yi - ?i)^2Where:
- MSE is the Mean Squared Error
- n is the number of observations
- yi represents the actual values
- ?i represents the predicted values
9. Mean Absolute Error
Mean Absolute Error (MAE) is a measure of errors between paired observations expressing the same phenomenon. The average of the absolute errors is a common way to measure the quality of an estimator and is always non-negative.
The formula for Mean Absolute Error is:
[ MAE = \frac{1}{n} \sum_{i=1}^{n} |actual_i - predicted_i| ]- To compute MAE:
- Calculate the absolute difference between each actual and predicted value.
- Sum up all the absolute differences.
- Divide the sum by the total number of observations ((n)).
- A lower MAE value indicates better model performance.
- MAE is advantageous as it retains the same scale as the data, making it easy to interpret.
- It is less sensitive to outliers compared to other error metrics like Mean Squared Error (MSE).
- When using Python to calculate MAE, you can utilize libraries like scikit-learn:
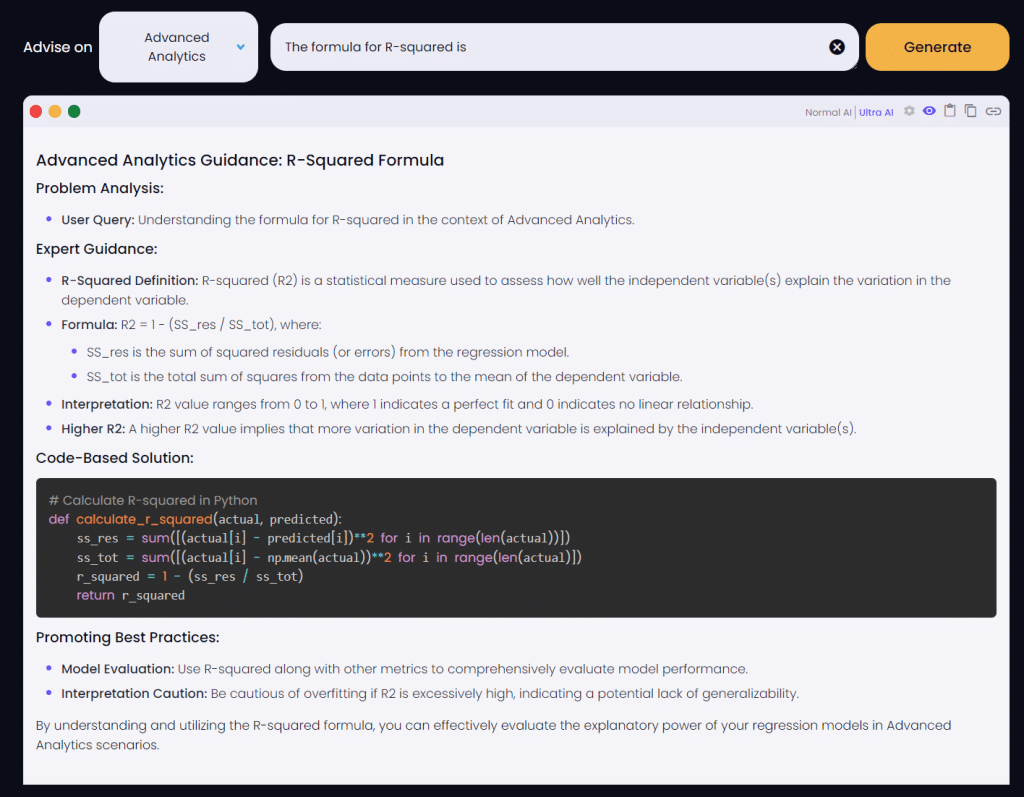
10. R-squared
R-squared, also known as the coefficient of determination, is a statistical measure of how close the data are to the fitted regression line. It is the percentage of the response variable variation that is explained by a linear model.
The formula for R-squared is:
def calculate_r_squared(actual, predicted):
ss_res = sum([(actual[i] - predicted[i])2 for i in range(len(actual))]) ss_tot = sum([(actual[i] - np.mean(actual))2 for i in range(len(actual)])
r_squared = 1 - (ss_res / ss_tot)
return r_squaredWhere:
- SSR is the sum of the squared differences between the predicted values and the mean.
- SST is the sum of the squared differences between the actual values and the mean.
- SSE is the sum of the squared differences between the actual values and the predicted values.
The value of R-squared can range from 0 to 1, with 1 indicating a perfect fit and 0 indicating that the model does not explain any of the variability of the response data around its mean.
4 Common Model Evaluation Techniques

In this section, we’ll go over 4 common model evaluation techniques:
- Train-Test Split
- K-Fold Cross-Validation
- Leave-One-Out Cross-Validation
- Bootstrapping
1. Train-Test Split
The train-test split is a simple and commonly used technique for model evaluation. It involves splitting the dataset into two parts: a training set and a test set.
The training set is used to train the model, and the test set is used to evaluate its performance.
The key to this technique is to ensure that the test set is completely independent of the training set.
2. K-Fold Cross-Validation
K-Fold Cross-Validation is a resampling technique that can be used to evaluate the performance of a machine learning model.
It involves dividing the training data into K equally sized partitions or folds, training the model on K-1 of the folds, and testing the model on the remaining fold.
This process is repeated K times, with each fold serving as the test set exactly once.
The performance of the model is then averaged over the K folds to obtain a single, more reliable estimate of the model’s performance.
3. Leave-One-Out Cross-Validation
Leave-One-Out Cross-Validation is a special case of K-Fold Cross-Validation where K is equal to the number of samples in the dataset.
This technique involves training the model on all but one sample and testing the model on the left-out sample.
This process is repeated for each sample in the dataset, and the performance of the model is then averaged over all the iterations.
Leave-One-Out Cross-Validation provides the most reliable estimate of a model’s performance but can be computationally expensive for large datasets.
4. Bootstrapping
Bootstrapping is a resampling technique that can be used to evaluate the performance of a machine learning model.
It involves creating multiple bootstrap samples by randomly sampling the training data with replacement.
The model is then trained on each bootstrap sample, and its performance is evaluated on the original test set.
This process is repeated a large number of times, and the performance of the model is averaged over the iterations to obtain a single, more reliable estimate of the model’s performance.
3 Advanced Model Evaluation Techniques

In this section, we’ll go over 3 advanced model evaluation techniques:
- Cross-Validation
- Grid Search
- Evaluation Curves
1. Cross-Validation
Cross-validation is a resampling technique that can be used to evaluate the performance of a machine learning model.
It involves splitting the training data into K equally sized partitions or folds, training the model on K-1 of the folds, and testing the model on the remaining fold.
This process is repeated K times, with each fold serving as the test set exactly once.
The performance of the model is then averaged over the K folds to obtain a single, more reliable estimate of the model’s performance.
2. Grid Search
Grid search is a hyperparameter optimization technique that can be used to improve the performance of a machine learning model.
It involves creating a grid of hyperparameter values and training the model with all possible combinations of these values.
The model’s performance is then evaluated using a cross-validation or train-test split, and the hyperparameters that result in the best performance are selected.
Grid search can be computationally expensive, especially for models with a large number of hyperparameters or a large training set.
3. Evaluation Curves
An evaluation curve is a graphical representation of the performance of a machine learning model as a function of one or more hyperparameters.
It can be used to visualize the impact of different hyperparameter values on the model’s performance and to identify the optimal values for these hyperparameters.
An evaluation curve is created by training the model with different hyperparameter values and evaluating its performance using a cross-validation or train-test split.
The performance is then plotted as a function of the hyperparameter values.
3 Tips for Evaluating Your Model

Here are some tips to help you evaluate your model more effectively:
- Understand your data: Before you start evaluating your model, make sure you understand the data you’re working with. Look for patterns, anomalies, or any issues that might affect the model’s performance.
- Use the right evaluation metric: Different problems require different evaluation metrics. Make sure you choose the right one for your specific use case.
- Be cautious with accuracy: While accuracy is an important metric, it can be misleading, especially with imbalanced datasets. Always consider other metrics like precision, recall, and F1-score.
- Consider a baseline model: It’s always a good idea to start with a simple baseline model. This will help you understand the problem better and give you a point of reference for evaluating more complex models.
- Test on real-world data: When possible, test your model on real-world data to see how it performs in a practical setting. This can help you identify any issues that might not be apparent in your training or validation data.
4 Best Practices for Model Evaluation

- Use multiple evaluation metrics: To get a comprehensive understanding of your model’s performance, it’s essential to use multiple evaluation metrics. This includes measures such as accuracy, precision, recall, F1-score, and area under the curve.
- Know your problem domain: Understanding the problem domain and the goals of your model is crucial. This will help you choose the right evaluation metrics and interpret their results in a meaningful way.
- Be aware of data quality: Your model’s performance heavily relies on the quality of the training data. Make sure the data is clean, relevant, and representative of the problem domain.
- Avoid data leakage: Data leakage can occur when information from the test set is unintentionally used in the training process. This can lead to overly optimistic evaluation results and a model that doesn’t generalize well to new data.
To avoid data leakage, ensure that the test set is completely separate from the training set, and be cautious when preprocessing data and creating features.
3 Challenges in Model Evaluation

Model evaluation in machine learning can be challenging, and here are 3 challenges you might encounter:
- Overfitting and Underfitting: Overfitting occurs when a model performs well on the training data but poorly on new, unseen data. It means that the model has learned to capture the noise in the training data instead of the underlying patterns. Underfitting, on the other hand, occurs when a model is too simple to capture the underlying patterns in the data. Both overfitting and underfitting can lead to inaccurate model evaluation results.
- Imbalanced Datasets: When one class in a classification problem is heavily outnumbered by the other, the dataset is considered imbalanced. This can lead to biased model evaluation, as accuracy might not be a good indicator of performance.
- Small Datasets: Model evaluation can be challenging with small datasets, as the results may not be statistically significant. It’s essential to be cautious when interpreting model performance in such cases.
Final Thoughts

Model evaluation is a crucial step in the machine learning pipeline. It allows you to assess your model’s performance and ensure it is effective in solving real-world problems. By understanding the concepts, metrics, and techniques we’ve covered in this article, you’ll be better equipped to evaluate your models and make informed decisions about their effectiveness.
Remember, model evaluation is not a one-time task but an ongoing process. As you continue to work on machine learning projects, you’ll encounter new challenges and opportunities to refine your skills. With dedication and practice, you’ll be able to develop models that can make accurate predictions and contribute to the advancement of machine learning applications.
For more help on your Machine Learning projects create your own Data Mentor account.
Frequently Asked Questions

What are the main steps in evaluating a machine learning model?
The main steps in evaluating a machine learning model are:
- Data Preparation: Clean, preprocess, and split your data into training and testing sets.
- Model Training: Train the model using the training set.
- Model Evaluation: Evaluate the model using the testing set and relevant evaluation metrics.
- Model Refinement: Make changes to the model if necessary and re-evaluate until you’re satisfied with the results.
What is the confusion matrix and how is it used to evaluate models?
A confusion matrix is a table that is used to evaluate the performance of a classification model. It compares the actual and predicted class labels for a set of test data.
The confusion matrix consists of four components:
- True Positives (TP)
- False Positives (FP)
- True Negatives (TN)
- False Negatives (FN)
These components can be used to calculate metrics such as accuracy, precision, recall, and F1-score, which provide more insights into the model’s performance.
What is the difference between precision, recall, and F1-score?
Precision measures the proportion of true positive predictions among all positive predictions made by the model, and it’s the measure of how many selected items are relevant. Recall, also known as sensitivity, measures the proportion of true positive predictions among all actual positive instances in the dataset, and it’s the measure of how many relevant items are selected.
The F1-score is a metric that combines precision and recall into a single value and is particularly useful when the dataset is imbalanced. It is calculated as the harmonic mean of precision and recall and gives equal weight to both metrics.
What are some common machine learning evaluation techniques?
Some common machine learning evaluation techniques are:
- Train-Test Split: The data is split into a training set and a testing set. The model is trained on the training set and evaluated on the testing set.
- Cross-Validation: The data is split into K folds, and the model is trained and tested K times, each time using a different fold as the testing set.
- Grid Search: A set of hyperparameters is defined, and the model is trained and tested for each combination of hyperparameters to find the best ones.
- Evaluation Curves: These are graphical representations of a model’s performance as a function of one or more hyperparameters.
What is the purpose of using ROC curves in model evaluation?
ROC curves are used to evaluate the performance of a binary classifier. They plot the true positive rate (TPR) against the false positive rate (FPR) at various threshold settings.
The area under the ROC curve (AUC) is a single scalar value that quantifies the overall performance of the classifier. A perfect classifier will have an AUC of 1, while a random classifier will have an AUC of 0.5.
ROC curves are particularly useful when you want to understand the trade-offs between sensitivity and specificity for different threshold settings of the classifier.